Scientist Finds Nature and Geometry Dancing to the Same Tune
For Salvatore Torquato, finding the answers to a few math problems came quite "naturally." This Princeton scientist has discovered that the natural arrangement of particles in their lowest energy state is a model for the solution to two abstract mathematical problems. His research illuminates the intimate relationship between geometry and physics, and he discloses a better understanding of low-temperature states of matter. The advancement of computer simulation techniques modeling these states of matter may lead to the design of novel materials for the U.S. Department of Energy (DOE), and a range of other applications arise for wireless communication systems, computer science, and the study of gravitational waves.
In the world of particle interactions, typically the easiest configuration to translate into equations is the "ground state." In this configuration, the system of particles is arranged to be as stable as possible, having its lowest possible energy. For instance, certain liquids become crystallized at a temperature of absolute zero. At this temperature, the molecules within the liquid are in their ground state, where they have the least energy and are essentially frozen in place.
Torquato realized that the methods and equations which represent ground state physics can also be used to solve the "covering" problem and the "quantizer" problem.
These are both known as optimization problems, in which a function is supposed to be maximized or minimized. Similarly, the equations representing the ground state of a physical system must be functions which minimize the system's energy.
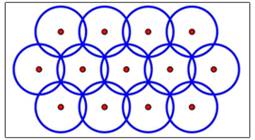
The covering problem is a puzzle that involves overlapping spheres. The objective is to find the most efficient way to arrange overlapping spheres so that they just cover a particular space. Mathematicians have used both theoretical and numerical optimization techniques to solve problems like this. Torquato's approach is unique in relating this problem to ground state particle interactions. The solutions can be applied to a number of topics including wireless communication and radiation therapy.
 Credit: Salvatore Torquato
Credit: Salvatore Torquato
An arrangement of circles (two-dimensional spheres) in a covering problem.
In the quantizer problem, the goal is to minimize what are known as "distance errors" in the positions of points when they are mapped to an "optimal point configuration." This might be easier to understand with an analogy. Imagine you are on a checkered picnic blanket. You brought along a bowl of cherries, which you spill onto the blanket. Suppose the optimal configuration would be for the cherries to land on the corners of the squares on the blanket. Certainly, the cherries will not spill such that each cherry lands on a corner. However, you could "map" each cherry to its nearest corner, taking note of the distance between the cherry's original position and the nearest corner. That distance is analogous to the "distance errors" of the quantizer problem. Sometimes, two cherries will both be closest to the same corner, but it would be best that they do not share a corner when they are mapped. So the objective of the quantizer problem in this case is to map the cherries in a way that will minimize the total distance errors. While we've used cherries to represent points here, Torquato's profound realization was that the optimal array of points in quantizer problems can be recast as an interacting system of particles in their ground state. Techniques for solving this type of problem can be used in the computer science behind digital communication, coding, and cryptography.
Torquato has shown that the best coverings and quantizers in high-dimensional space might require disordered arrangements, the opposite of what occurs in our own three-dimensional space where the best solutions are thought to be orderly arrangements. For instance, in high-dimensional space, the optimal arrangement may be more complicated than the checkerboard pattern of a picnic blanket. While high-dimensional space may seem abstract, the mathematics can be applied to high-dimensional data sets, which scientists do encounter in the real world. For example, high-dimensional mathematics may be useful in creating software tools which can sort through the data sets being collected in the attempt to detect gravitational waves. These waves are ripples through spacetime, and they are part of Einstein's General Theory of Relativity. They are supposedly created when very large objects, such as black holes, move in certain ways. Gravitational waves have not yet been discovered experimentally.
In his paper, Torquato explains how his reformulation of the solutions to the covering and quantizer problems relates to the sphere-packing and number-variance problems. The sphere-packing problem requires finding the densest possible arrangement of non-overlapping spheres in a particular space, while the number-variance problem is related to an optimization problem in number theory.
It was already known that particle systems and sphere-packing can be represented with similar mathematics, but Torquato's application of ground state particle physics to the covering and quantizer problems is unprecedented. His reformulations may be particularly useful in creating computer simulations of low-temperature states of matter, which will be useful for designing materials for DOE.
Torquato's work, supported by DOE's Office of Basic Energy Sciences, provides another example of how nature and geometry dance to the same tune. "This paper describes what I believe to be a wonderful example of the deep interplay between geometry and physics," Torquato said. While mathematics often explains physics, his work exemplifies the way in which the fundamental physics of the universe can complimentarily reveal answers to profound mathematical questions.
This article was written by Abigail Pillitteri
For more information on the findings, please go to:
http://pre.aps.org/abstract/PRE/v82/i5/e056109, http://www.princeton.edu/main/news/archive/S28/99/37K57/
For more information on the DOE Office of Science, please visit: http://www.science.energy.gov/

